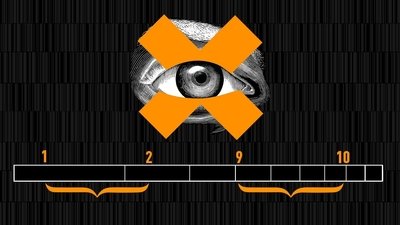
Benford’s Law
Episode 1 • Sep 23, 2021
Frank Benford observed that the number one seems to pop up a lot in both in the supermarket and on tax bills. In understanding this law, it helps to simply look at the world from a different perspective.
Math is an exotic and confusing country. We speak a bizarre language, full of homeomorphisms, differential varieties, transfinite numbers. But we also find epic landscapes, dizzying ideas and even, sometimes, useful things!
20 episodes total
Status
Returning Series
First Aired
2021
Rating

8.5/10
2 votes • HD
People
Cast information is not available for this show.
Episodes

Episode 1 • Sep 23, 2021
Frank Benford observed that the number one seems to pop up a lot in both in the supermarket and on tax bills. In understanding this law, it helps to simply look at the world from a different perspective.

Episode 2 • Sep 23, 2021
Speed is such a common term that it's easy to forget how much of a role maths plays in understanding it. Until three or four centuries ago, there was no speed at all. It was only since the Renaissance that the concept of movement crept into the world of mathematics, thanks to calculus and Isaac Newton.

Episode 3 • Sep 23, 2021
A circle is also a triangle and a triangle is a square. Sound impossible? Not in the realm of topology, which even applies to 3-dimensional spaces and anything from donuts, UFOs and potatoes. The discipline's inventor, Henri Poincaré, created one of the most difficult problems in mathematics.

Episode 4 • Sep 23, 2021
In this episode of our travels in the land of maths, we are heading towards Infinity. And even beyond, because infinity comes in many sizes. That may seem strange, but Georg Kantor and his set theory will help us come to terms with this maths concept of dizzying scale.

Episode 5 • Sep 23, 2021
In this episode, we look at the relationship between maths and truth. Maths is meant to be certain, either right or wrong. Turns out, it’s not that simple. For Gödel's theorem has proved that there are “undecidable” theories, which one can neither prove nor disprove.

Episode 6 • Sep 23, 2021
Two prisoners must choose between cooperation and betrayal without consulting each other. This famous prisoner's dilemma that will take us to the heart of game theory. We think mathematically about a very philosophical question: is it in our interest to collaborate with others?

Episode 1 • Oct 10, 2023
The Monty Hall paradox, named after a game show from the 60s, concerns the way in which information acquired during the course of a game modifies (or not) the winning statistics. Theoretically solved, the question is so disturbing to our worldview that it continues to be the subject of passionate debate to this day.

Episode 2 • Oct 10, 2023
Statistics seem, almost by their very nature, to convey a positivist message. They are, in fact, a formidable tool in the attempt to master the complexity of the real world... But numerous "biases" threaten any discourse that refers to them without care: an over-simplistic reading of the figures can lead us - for example - to confuse correlation with causation... And more complex phenomena (notably Simpson's paradox) can distort conclusions that seem objective.

Episode 3 • Oct 10, 2023
For centuries, geometry was based on Euclid's postulates, which seemed eternal and irrevocable. However, one of the postulates (the fifth) has always seemed "a little less natural" than the others, and hundreds of mathematicians have tried in vain to do without it by deducing it from the other postulates. In the mid-19th century, Bernhard Riemann came up with a novel idea: let's imagine it's false! This was the birth of "non-Euclidean geometries", which would later have major applications in physics.

Episode 4 • Oct 10, 2023
A tessellation is a way of covering a plane with a repeating pattern... Basically, it's like creating wallpaper. In 1975, Marjorie Rice (1923- 2017), a mother and amateur mathematician, read an article by Martin Gardner in Scientific American that listed ALL possible "pentagonal tessellations" in the plane. A mathematician had just proved that the list was complete. Except that Marjorie, working alone at home, found 4 new ones... The theorem was wrong!

Episode 5 • Oct 10, 2023
The question is how to make a network that is both "economical" and "robust" without taking up too much space. This is a theoretical question worked on by the great Russian mathematician Andrey Kolmogorov (1903-1987). But this theoretical question also conditions the way in which we can build a computer network or... a human brain: to be intelligent without having a big head, you need a neural network that is efficient BUT ALSO compact! Mention Szemeredi lemma?

Episode 6 • Oct 10, 2023
To begin with, there are the five "Platonic solids" beloved of geometers: the cube, the tetrahedron, the octahedron, the dodecahedron and the icosahedron. But why stop at the 3 dimensions of ordinary space? Alicia Boole Stott has devoted her life to finding regular solids in dimension 4... and she's found them! A journey into unsuspected mathematical regions.
Recommendations
2018 • TV Show

2015 • TV Show

2018 • TV Show

2008 • TV Show
1971 • TV Show

2011 • TV Show

2014 • TV Show

2001 • TV Show

2014 • TV Show

2014 • TV Show

2012 • TV Show

2004 • TV Show